Tag or Tally attached at every 10th link which represents distances from both ends of the chain

The stationary distance, or mearings of ground, are measured either by Mr. Gunter's chain of four poles or perches, which consist of 100 links; (and this is the most natural division) or by one of 50 links, which contains two poles or perches: but because the length of a perch differs in many places, therefore the length of chains and their respective links will differ also.

The English statute-perch is 5 1/2 yards, the two-pole chain is 11 yards, and the four-pole one is 22 yards; hence the length of a link in a statute-chain is 7.92 inches.

There are other perches used in different parts of England, as the perch of woodland measure, which is 6 yards; that of church-land measure, which is 7 yards (or the same with the plantation perch) and the forest measure perch which is 8 yards.

The Irish or plantation perch, is 7 yards, as before; the two-pole chain is 14; and the four-pole one is 28 yards: hence the length of a link in a

plantation chain is 10.08 inches.

The Scotch perch is 18 1/2 feet, or 6 1/4 yards, or 6 Scot's ells. In the shire of Cunningham in Scotland, their perch is 18 3/4 feet, and this perch is used in some few places in the north part of this kingdom, as the statute perch is in some other parts.

For the more ready reckoning the links of a four-pole chain, there is a large ring, or sometimes a round piece of brass fixed at every 10 links; and at 50 links, or in the middle, there are two large rings. In such chains as have a brass piece at every 10 links, there is the figure 1 on the first piece, 2 on the second, 3 on the third, &c. to 9. By leading therefore that end of the chain forward, which has the least number next it, he who carries the hinder end may easily determine any number of links: thus, if he has the brass piece number 8, next to him, and 6 links more in a distance, that distance is 86 links. After the same manner 10 may be counted for every large ring of a chain which has not brass pieces on it; and the number of links is thus readily determined.

The two-pole chain has a large ring at every 10 links, and in its middle, or at 25 links, there are two large rings; so that any number of links may be the more readily counted off, as before.

The surveyor should be careful to have his chain measured before he proceeds on business, for the rings are apt to be open by frequent using it, and its length is thereby increased, so that no one can be too circumspect in this point.

In measuring a stationary distance, there is an object fixed in the extreme point of the line to be measured; this is a direction for the hinder chainman to govern the foremost one by, in order that the distance may be measured in a right line; for if the hinder chainman causes the other to cover the object, it is plain the foremost is then in a right line towards it. For this reason it is necessary to have a person that can be relied on, at the hinder end of the chain, in order to keep the foremost man in a right line; and a surveyor who has no such person, should chain himself. The inaccuracies of most surveys arise from bad chaining, that is, from straying out of the right line, as well as from other omissions of the hinder chainman: no person, therefore, should be admitted at the hinder end of the chain, of whose abilities in this respect, the surveyor was not previously satisfied and convinced; since the success of the survey, in a great measure, depends on his care and skill.

In setting out to measure any stationary distance, the foreman of the chain carries with him 10 iron pegs pointed, each about ten inches long; and when he has stretched the chain to its full length, he at the extremity thereof sticks one of those pegs perpendicularly in the ground; and leaving it there, he draws on the chain till the hinder man checks him when he arrives at that peg; the chain being again stretched, the foreman sticks down another peg, and the hind man takes up the former; and thus they proceed at every chain's length contained in the line to be measured, counting the surplus links contained between the last peg, and the object at the termination of the line as before: so that the number of pegs taken up by the hinder chainman, expresses the number of chains; to which, if the odd links be annexed, the distance line required in chains and links is obtained, which must be registered in the field book, as will hereafter be shewn.

If the distance exceeds 10, 20, 30, &c. chains, when the leader's pegs are all exhausted, the hinder chainman, at the extremity of the 10 chains, delivers him all the pegs; from whence they proceed to measure as before, till the leader's pegs are again exhausted, and the hinder chainman at the extremity of these 10 chains again delivers him the pegs; from whence they proceed to measure the whole distance line in the like manner; then it is plain, that the number of pegs the hinder chainman has, being added to 10, if he had delivered all the pegs once to the leader, or to 20 if twice; or to 30 if thrice, &c, will give the number of chains in that distance; to which if the surplus links be added, the length of the stationary distance is known in chains and links.

It is customary, and indeed necessary, to have red, or other coloured cloth fixed to the top of each peg, that the hinder man at the chain may the more readily find them; otherwise, in chaining thro' corn, high grass, briars, rushes, potatoes, &c. it would be extremely difficult to find the pegs which the leader puts down: by this means no time is lost, which otherwise must be, if no cloths are fixed to the pegs, as before.

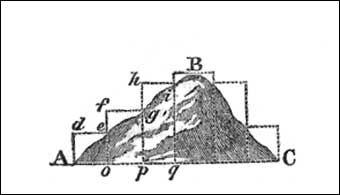
It will be necessary here to observe, that all slant, or inclined surfaces, as sides of hills, are measured horizontally, and not on the plane or surface of the hill, and is thus effected.

Let ABC be a hill, the hindmost chainman is to hold the end of the chain perpendicularly over the point A (which he can the better, effect with a plummet and line, than by letting a stone drop, which is the most usual) as d is over A, while the leader puts down his peg at e: the eye can direct the horizontal position near enough, but if greater accuracy were required, a quadrant applied to the chain would settle that. In the same manner the test may be chained up and down; but in going down it is plain the leader of the chain must hold up the end thereof, and the plummet thence suspended, will mark the point where he is to stick his peg. The figure is sufficient to render the whole evident; and to shew that the sum of the chains will be the horizontal measure of the base of the hill; for de=Ao, fg=op, hi=pq, &c. therefore de+fg+hi, &c. =Ao+op+pq, &c. =AC, the base of the hill. If a whole chain cannot be carried horizontally, half a one, or less, may, and the sum of these half chains or links, will give the base, as before.

If the inclined side of the hill be the plane surface, the angle of the hill's inclination may be taken, and the slant height may be measured on the surface; and thence (by case 1. of right-angled trigonometry) the horizontal line answering to the top, may be found; and if we have the angle of inclination given on the other side, with those already given; we can find the horizontal distance across the hill, by case 2. of oblique trigonometry.

All inclined surfaces are considered as horizontal ones; for all trees which grow upon any inclined surface, do not grow perpendicular thereto, but to the plane of the horizon: thus if Ad, ef, gh, &c. were trees on the side of a hill, they grow perpendicular to the horizontal base AC, and not to the surface AB: hence the base will be capable to contain as many trees as are on the surface of the hill, which is manifest from the continuation of them thereto. And this is the reason that the area of the base of a hill, is considered to be equal in value to the hill itself.

Besides, the irregularities of the surfaces of hills in general are such, that they would be found impossible to be determined by the most able mathematicians. Certain regular curve surfaces have been investigated with no small pains, by the most eminent; therefore an attempt to determine in general the infinity or irregular surfaces which offer themselves to our view, to any degree of certainty, would be idle and ridiculous, and for this reason also, the horizontal area is only attempted.

Again, if the circumjacent lands of a hill be planned or mapped, it is evident we shall have a plan of the hill's base in the middle: but were it possible to put the hill's surface in lieu thereof, it would extend itself into the circumjacent lands, and render the whole an heap of confusion: so that if the surfaces of hills could be determined, no more than the base could be mapped.

Roads are usually measured by a wheel for that purpose, to which there is fixed a machine, at the end whereof there is a spring, which is struck by a peg in the wheel, once in every rotation; by this means the number of rotations is known. If such a wheel, were 3 feet 4 inches in diameter, one 10 1/2 one rotation would be 10 1/2 feet, which is half a plantation perch; and because 320 perches make a mile, therefore 640 rotations will be a mile also; and the machinery is so contrived, that by means of a hand, which is carried round by the work, it points out the miles, quarters, and perches, or sometimes the miles, furlongs, and perches.

Or roads may be measured by a chain more accurately: for 80 four-pole, 160 two-pole chains, or 320 perches, make a mile as before: and if roads are measured by a statute chain, it will give you the miles English, but if by a plantation chain, the miles will be Irish. Hence an English mile contains 1760, and an Irish mile 2240 yards; and because 14 half hards is an Irish, and 11 half yards is an English perch, therefore 11 Irish perches, or Irish miles, are equal to 14 English ones.

The place was now newly named Williamsburg, after the reigning monarch, King William, and the first survey was made by Thoedorick Bland. Two ports, each about a mile distant from the town, were laid out -- one called Princess Anne Port on Archer's Hope or College Creek, about five miles from James River, and the other called Queen Mary's Port on Queen's Creek, about the same distance from York River. The body of the town occupied 220 acres; Princess Anne Port 23 acres, 37 1/2 poles, and Queen Mary's Port 14 acres, 71 1/4 poles. So that the whole area of the town and ports, (including the two roads leading to the latter embracing 25 acres, 86 3/4 poles) was 283 acres, 35 1/2 poles. The main street (called in 1705, Duke of Gloucester Street, in honor of Queen Anne's eldest son) followed partially the course of the old Middle Plantation horse path, and was 99 feet wide and seven-eigths of a mile long from the college to the east end of town, where the capitol building afterwards was placed.